
1. 문제 정의
입력으로 주어진 그래프가 이분 그래프인지 아닌지를 판별하는 프로그램을 작성하는 문제이다.
그래프의 정점의 집합을 둘로 분할하여 각 집합에 속한 정점끼리는 서로 인접하지 않도록 분해할 수 있을 때의 그래프를 이분 그래프라 하는데, 솔직히 문제만을 보고서는 이분 그래프가 뭔지 감이 잘 오지 않는다.

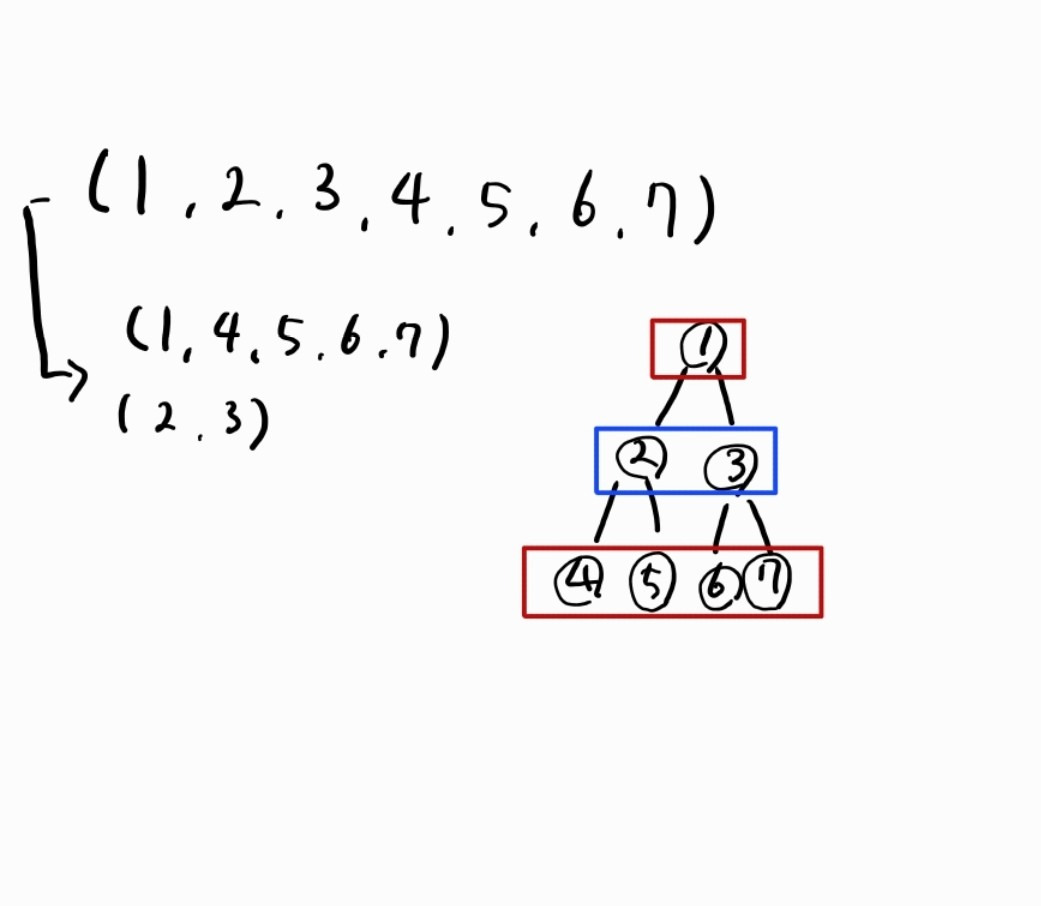
다음은 이분 그래프에 대한 이해를 돕기 위한 그림이다.
이분 그래프는 인접한 노드 끼리의 색상이 서로 다른 그래프로 이해하고 일단 넘어가도록 하자.
2. 풀이 방식
for _ in range(K):
V, E = map(int, input().split())
graph = [[] for _ in range(V+1)] # 그래프 초기화
visited = [False] * (V+1) # 방문 표시
colors = [0] * (V+1) # 색상 표시
# 그래프 생성
for _ in range(E):
a, b = map(int, input().split())
graph[a] += [b]
graph[b] += [a]문제의 입력으로 먼저 테스트 케이스 개수 K가 주어진다. 이후 테스트 케이스의 첫 번째 줄에는 정점의 개수 V와 간선의 수 E가 주어지고, 간선에 대한 정보인 인접한 두 정점의 번호가 주어진다.
주어진 정보를 이용해 먼저 그래프를 생성한다.
또한 그래프의 방문 정보를 기록하기 위한 리스트와 색상 정보를 담는 리스트를 생성한다.
앞서 설명했듯이 나는 정점의 색의 일치 여부를 판단하는 프로그램을 설계할 것이다. 따라서 깊이 우선 탐색(DFS) 알고리즘을 활용하여 함수를 정의한다. 함수의 인자로 정점의 번호와 색을 갖는다.
def dfs(num, color): # color : 1 = red / -1 = blue
visited[num] = True
colors[num] = color # 임의의 색상 부여 (1 = red)
for ix in graph[num]:
if not (visited[ix]):
a = dfs(ix, -color) # 방문하지 않은 정점인 경우 반대 색상 부여 (-1 = blue)
if not a: # 탐색 결과가 false면 false 리턴
return False
elif (colors[ix] == colors[num]): # 현재 정점과 다음 정점의 색상이 같은 경우 false 리턴
return False
return True먼저 탐색 시작 정점의 색을 저장한다. 이후 다음 정점이 방문하지 않은 정점이라면 DFS 알고리즘에 의해 정점의 다음 정점의 DFS 함수를 호출한다.
# 각 정점을 시작점으로 두고 탐색
for i in range(1, V+1):
if not (visited[i]): # 방문하지 않은 정점인 경우만
result = dfs(i, 1) # (1 = red, -1 = blue)
if not result: # 탐색 리턴값이 false면 break
break
print("YES" if result else "NO")만약 방문을 한 정점이라면, 색상 일치 여부를 판단한다. 색상이 같을 경우, 인접한 정점의 색상이 같기 때문에 이 그래프는 이분 탐색 그래프가 아니다. 따라서 False를 리턴한다.
또한 다음 정점을 탐색하는 과정에서, 그 다음의 정점과 색이 같을 경우(즉, False를 리턴한 경우), 마찬가지로 False 리턴.
모든 조건을 만족할 경우 True를 리턴
그래프의 모든 정점에 대해 DFS 함수 호출, 이때 색상은 임의의 값 (red = 1, blue = -1로 지정)을 넣어주었다.
함수의 리턴값에 따라 결과를 출력한다.
🗒️최종 제출 코드
# 1707 이분 그래프
import sys
input = sys.stdin.readline
sys.setrecursionlimit(1000000)
K = int(input())
def dfs(num, color): # color : 1 = red / -1 = blue
visited[num] = True
colors[num] = color # 임의의 색상 부여 (1 = red)
for ix in graph[num]:
if not (visited[ix]):
a = dfs(ix, -color) # 방문하지 않은 정점인 경우 반대 색상 부여 (-1 = blue)
if not a: # 탐색 결과가 false면 false 리턴
return False
elif (colors[ix] == colors[num]): # 현재 정점과 다음 정점의 색상이 같은 경우 false 리턴
return False
return True
for _ in range(K):
V, E = map(int, input().split())
graph = [[] for _ in range(V+1)] # 그래프 초기화
visited = [False] * (V+1) # 방문 표시
colors = [0] * (V+1) # 색상 표시
# 그래프 생성
for _ in range(E):
a, b = map(int, input().split())
graph[a] += [b]
graph[b] += [a]
# 각 정점을 시작점으로 두고 탐색
for i in range(1, V+1):
if not (visited[i]): # 방문하지 않은 정점인 경우만
result = dfs(i, 1) # 임의의 색상 1 (or -1) 부여
if not result: # 탐색 리턴값이 false면 break
break
print("YES" if result else "NO")
3. 후기
이분 탐색을 활용하는 그래프 문제인가 싶었지만, 이분 그래프라는 새로운 개념에 대해 알게되었다.
'이분 그래프'라는 단어 하나만 들었을 때에는 뭔지 기억이 가물가물 했는데, 구글에 검색해보니 그림이 딱 나온걸 보고 '아 이거구나!' 싶었다. ㅋㅋ 역시 알고리즘은 그림으로 공부하는게 기억에 오래 남는듯 하다.
'Coding-Test > 백준' 카테고리의 다른 글
| [Python] 11725 - 트리의 부모 찾기 (0) | 2025.02.28 |
|---|---|
| [Python] 1918 - 후위 표기식 (1) | 2025.02.27 |
| [Python] 2667 - 단지번호붙이기 (0) | 2025.01.27 |
| [Python] 1697 - 숨바꼭질 (0) | 2025.01.21 |
| [Python] 1260 - DFS와 BFS (1) | 2025.01.20 |